Matematika Diskrit : Relasi, Sifat Relasi, dan Contoh Soal

Struktur Diskrit : Pohon Merentang, Kruskal's Algorithm, dan Prim's Algorithm

Spanning Trees

Let G be a simple graph. A spanning tree of G is a subgraph of G that is a tree containing every vertex of G. A simple graph is connected if and only if it has a spanning tree. Applied in IP multitasking. 

Exercise

Find a spanning tree for the following graphs.

Minimum Spanning Trees

A minimum spanning tree in a connected weighted graph is a spanning tree that has the smallest possible sum of weights of it edges. 

Two algorithms can be used : 

• Prim’s Algorithm by Robert Prim, 1957 
• Kruskal’s Algorithm by Joseph Kruskal, 1956 

Prim’s Algorithm

1. Chose an edge with the least weight. 
2. Include it in spanning tree, T. 
3. Select an edge of least weight that is incident with a vertex of an edge in T. 
4. If it does not create a cycle (simple circuit) with the edges in T, then include it in T; otherwise discard it. 
5. Repeat STEPS 3 and 4 until T contains n-1 edges.

There may be more than one minimum spanning tree for a given connected weighted simple graph. If there are two edges with similar smallest weight, chose either one.

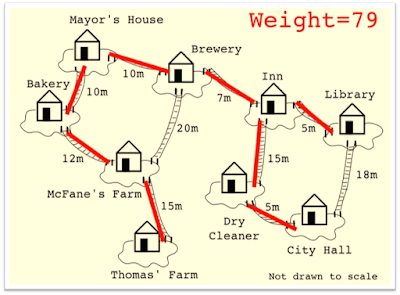
Example: Prim’s Algorithm

Kruskal’s Algorithm

1. Arrange the edges in G in increasing order. 
2. Chose an edge with the minimum weight. 
3. Include it in spanning tree, T. 
4. Add an edge of least weight to T. 
5. If it does not create a cycle (simple circuit) with the edges in T, then include it in T; otherwise discard it. 
6. Repeat STEPS 4 and 5 until T contains n-1 edges. 

There may be more than one minimum spanning tree for a given connected weighted simple graph. If there are two edges with similar smallest weight, chose either one. 

Example: Kruskal’s Algorithm

Sumber

Slide Strukdis : Spanning Tree

http://informatika.unpar.ac.id/