Matematika Diskrit : Relasi, Sifat Relasi, dan Contoh Soal

Pengantar Logika : Proposisi, Hubungan Antar Proposisi, Definisi Term, Sifat Term, dan Contoh Soal

PENGERTIAN DAN KEPUTUSAN

PENGERTIAN

• •Pikiran melakukan abstraksi/aprehensi atas hakikat dari suatu hal/benda yang konkrit
• •Bentuknya berupa Konsep
• •Verbalisasi dari konsep adalah Term.

KEPUTUSAN

• •Rangkaian pengertian
• •Ada pengakuan dan pengingkaran: mengakui/mengiyakan/afirmasi dan mengingkari/tidak/negasi
• •Term subjek dan term predikat
• •Keputusan yang diverbalkan menghasilkan Proposisi
• •Kalimat informatif/kalimat berita/kalimat deklaratif (bukan kalimat tanya/seruan)
• •Walaupun proposisi dirumuskan dengan sebuah kalimat tetapi proposisi itu tidak boleh begitu saja diidentikkan dengan kalimat.

DEFINISI TERM

• Term adalah verbalisasi dari sebuah konsep/ide/pengertian dalam bentuk kata atau rangkaian kata
• Term = Kata (tapi tidak semua kata adalah term)
• Kategorimatis merupakan kata memiliki pengertian sendiri (saya, rumah, sekolah)
• Sin-kategorimatis merupakan kata yang tidak memiliki pengertian (biru, bagus, wah, yang, manis

Klasifikasi Term

A. Dilihat dari jumlah kata yang menyusun

• Term tunggal : satu kata
• Term majemuk : lebih dari satu kata

B. Dilihat dari sudut fungsinya dalam proposisi

• Term subjek : sebagai subjek dalam proposisi
• Term predikat : sebagai predikat dalam proposisi
• Term Tengah : Penghubung term mayor dan term minor (silogisme)

C. Dilihat dari luas/cakupan

• Term singular : individu/barang (satu/tertentu)
• Term partikular : sebagian dari keseluruhan (beberapa)
• Term universal : keseluruhan (tanpa kecuali)

D. Dilihat dari Sifat Term

• Term berdistribusi dan tidak berdisribusi. 
• Term dikatakan berdistribusi jika pengertiannya mencakup semua anggota (universal/keseluruhan). 
• Contoh: mahasiswa adalah orang terpelajar. Sedangkan term yang tidak berdistribusi meliputi sebagian dari semua anggota, satu atau lebih (partikular). Contoh: Sebagian wanita menginginkan kekayaan

• Term individual dan kolektif. 
• Disebut individual jika pengertian term dikenakan pada anggota atau individu satu demi satu. Sedangkan kolektif adalah pengertian yang terkandung dalam term tidak dapat dikenakan kepada anggota atau invidu satu demi satu melainkan sebagai suatu keseluruhan. 
• Contoh: keluarga, bangsa, rombongan, masyarakat, team, kesebalasan, korps

Beberapa pedoman untuk menentukan luas term apabila term kolektif posisinya sebagai subjek dalam proposisi 

• Jika berdiri sendiri maka luas/cakupannya universal: contoh: keluarga, masyarakat, kelompok
• Jika menunjuk pada satu kelompok/komponen tertentu maka luas/cakupannya singular. Contoh: Keluarga Sinaga, keluarga cemara, masyarakat desa Cidadap atau menunjukkan pada nama kelompok/grup tertentu

E. Dilihat dari Arti term

• Univok: 
• Term yang bunyi dan artinya sama. 
• Contoh buah impor - buah lokal, uang korupsi-uang haram

• Ekuivok: 
• Term yang bunyi sama tapi beda arti. 
• Contoh, bisa = racun ular berbeda dengan bisa = mampu

• Analog: 
• Term yang bunyi sama tp arti bisa sama bisa juga berbeda. 
• Contoh: cantik wajah – cantik hati

Proposisi adalah verbalisasi dari keputusan (menghubungkan 2 konsep/pengertian/term)

“Semua kuda adalah binatang”

      S                   P

keputusan mengiyakan/mengakui (Afirmasi):
Konsep “Kuda” (S) semuanya termasuk ke dalam konsep “binatang “(P)

“Semua kuda (adalah) bukan tumbuhan”

      S                                 P

Keputusan menyangkal/mengingkari (Negasi):
Konsep “kuda” (S) semuanya tidak termasuk ke dalam konsep “tumbuhan” (P)

Unsur-unsur Proposisi

• Quantifier (Q) 
• perkataan yang menunjukkan jumlah anggota kelas (cakupan/luas) yang berkedudukan sebagai subyek

• Term Subyek (S) 
• term yang di dalam proposisi dinyatakan termasuk atau tidak termasuk ke dalam kelas yang lainnya (predikat)

• Kopula (K) 
• perkataan sebagai bagian dari proposisi yang menunjukkan hubungan antara term subyek dan predikat, yang menunjukkan apakah subyek termasuk atau tidak termasuk ke dalam predikat (afirmasi atau negasi)

• Predikat (P) 
• term yang di dalam proposisi berkedudukan sebagai term yg ke dalamnya term subyek dinyatakan termasuk atau tidak termasuk

Quantifier merujuk pada kuantitas Term Subjek (Luas/Cakupan Term Subjek)

Problem Menentukan Quantifier

Singularitas sebenarnya tidak menyatakan jumlah, tetapi “yang tertentu” merupakan “satu / tertentu”. Proposisi yang luasnya singular dianggap memiliki cakupan universal (dalam silogisme)

Jakarta adalah ibukota negara Indonesia.

Makanan ini enak.

Pintu itu sulit dibuka.

Matahari terbit di timur.

Diatas merupakan cakupan universal

Latihan 1

Tentukanlah quantifiernya !

1. Pensil itu milikku
2. Anita adalah mahasiswa unpar
3. Tuhan adalah pegangan hidupku
4. DPR adalah wakil rakyat
5. Mahasiswa UNPAR cerdas
6. Yang mencuri berdosa

Problem Menentukan Quantifier jika quantifiernya eksplisit maka perlu dilihat konteksnya

Perhatikan Contoh !

• Manusia adalah makhluk berakal budi (universal)
• Mahasiswa Unpar memiliki mobil. (singular menjadi  universal)
• Mahasiswa yang tidak membawa KTM sewaktu ujian dilarang masuk (partikular)
• Semua mahasiswa mau tidak mau harus ujian (universal)
• Lima mahasiswa kelas X mendapat penghargaan (singular menjadi universal)
• Satu orang mahasiswa lulus (singuar menjadi universal)

Latihan 2

Tentukan Jenis Proposisinya!

1. Semua pegawai negeri adalah abdi negara.
2. Keluarga Situmorang rajin beribadah
3. Sebagian pramuka adalah lulusan sekolah dasar.
4. Sebagian prajurit tidak dapat kembali ke markas dengan cepat.
5. Masyarakat Indonesia hidup dalam kemajemukan
6. Sebagian balita belum bisa berlari dengan baik.
7. Hampir semua satpam adalah lulusan SMA
8. 6 dari 10 orang di ruangan kurang bisa memanfaatkan waktu.
9. Tiga kendaraan polisi dirusak.
10. Sejumlah warga dilaporkan tertembak peluru karet.
11. Korps prajurit TNI adalah orang yang siap berkorban demi keutuhan NKRI
12. 100% mahasiswa lulus dengan hasil yang memuaskan

Kopula

Kopula berfungsi sebagai penghubung term subjek dan term predikat untuk menyatakan/mengafirasi/menegasi (syarat keputusan). Kopula merujuk pada kualitas hubungan subjek dan predikat

• Afirmatif terjadi pengakuan predikat terhadap subjek. Bentuk verbalnya “adalah” 
• Contoh: Ahli hukum (adalah) mengenal keadilan

• Negatif terjadi pengingkaran predikat terhadap subjek. Bentuk verbalnya ”(adalah) tidak “ atau “(adalah) bukan” 
• Contoh: Ahli hukum (adalah) tidak mengenal keadilan

Latihan 3

• Saya sakit
• Anak yang kemarin datang ke rumah saya dengan mengendarai sepeda motor, kesrempet mobil tadi pagi
• Masih ada orang yang membuang sampah sembarangan

Perhatian ! 

Perlu melakukan standardisasi untuk mengidentifikasi/analisis unsur-unsur dalam proposisi

Problem Menentukan Kopula

Kopula tersembunyi (tidak disebut secara eksplisit) terletak di antara S & P (hubungan afirmasi/negasi)

Perhatikan contoh berikut:

• Semua mahasiswa yang membawa KTM tidak boleh masuk ruangan.
• Semua mahasiswa yang tidak membawa KTM boleh masuk ruangan.
• Semua mahasiswa yang tidak membawa KTM tidak boleh masuk ruangan.
• Semua mahasiswa dilarang masuk.
• Semua mahasiswa tidak boleh masuk. 
• Semua mahasiswa belum masuk. 
• Semua mahasiswa kurang perasa.

Berdasarkan identifikasi quantifier (kuantitas) dan kopula (kualitas) maka menghasilkan 4 model proposisi sederhana/proposisi tradisional :

Bagaimana dengan Proposisi ini ?

• Tak satu pun manusia tidak bebas
• Tidak ada tim sepak bola ingin kalah
• Tidak semua mahasiswa lulus
• Tidak semua Orang Sunda bukan pencinta Persib

Ekuipolensi Proposisi

• Negasi Ganda
• Proposisi ini berkualitas afirmatif (pengingkaran ganda = pengakuan)
• Universal Afirmatif/A
• Tidak ada (tidak satupun) S adalah bukan P
• Semua S adalah P
• Tak satu pun manusia tidak bebas
• Semua manusia tidak tidak bebas
• Semua manusia bebas

• Negasi bersamaan dengan “ada”
• Universal Negative/E
• Tidak ada S adalah P
• Semua S adalah bukan P
• Tidak ada tim sepak bola yang ingin kalah
• Semua tim sepakk bola tidak ingin kalah

• Kata “Tidak” di depan penunjuk kuantitas/quantifier
• Partikular Negatif/ O
• Tidak semua S adalah P
• Beberapa S adalah bukan P
• Tidak semua mahasiswa lulus
• Beberapa mahasiswa tidak lulus

• Tidak semua S adalah bukan P 
• Berlaku aturan negasi ganda menjadi Partikular Afirmatif/I 
• Beberapa S adalah P

PERINGATAN CATATAN KHUSUS !

Proposisi yang belum memiliki bentuk standar (tradisional) perlu diubah dahulu menjadi bentuk standar (tradisional)

A, E, I, atau O

Bentuk-bentuk yang belum standar antara lain:

• Singular
• Ekuipolensi
• Quantifier/ kopula tersembunyi

Hati-hati dengan negasi term (tidak -, non -, tak - )

Latihan 4

Tentukan Jenis Proposisi di bawah ini!

1. Semua orang yang tidak-mendapatkan izin dibiarkan masuk ruangan itu.
2. Tidak ada demonstran yang tidak militan
3. Sebagian mahasiswa yang bukan-berasal dari Jakarta kesulitan mendapatkan izin tinggal di kota tersebut.
4. Tak satu pun mahasiswa tidak mengikuti kuliah logika
5. Para pelaku korupsi dihukum penjara seumur hidup
6. Tidak ada gading tak-retak.
7. Seluruh peserta Asean Games mendapatkan bonus
8. Semua yang bukan-anggota kelas logika tidak tidak-diperbolehkan duduk di kursi itu.

LUAS TERM

Perhatikan proposisi di bawah ini!

1. Semua orang Indonesia adalah orang Asia
2. Semua manusia dapat berpikir kritis
3. Asep adalah orang Indonesia
4. Sebagian mahasiswa UNPAR adalah orang Sunda
5. Semua orang Indonesia adalah bukan orang Eropa
6. Agnes Monica adalah bukan Siti Badriah

Catatan :

• Untuk proposisi afirmatif baik singular, universal dan partikular (A dan I) luas term predikat selalu partikular
• Dalam proposisi negatif baik singular, universal dan partikular luas term predikatnya selalu universal
• Dalam proposisi negatif, luas term predikatnya universal. Subjek dipisahkan dari predikat dan sebaliknya.

TABEL LUAS/CAKUPAN TERM

SYARAT SEBUAH TERM TERDISTRIBUSI

•Sebuah term dikatakan terdistribusi jika term itu ditujukan kepada semua anggota kelas yang berkedudukan sebagai term tersebut di dalam proposisi yang bersangkutan (luas cakupan/sebaran)

•Sebuah term dikatakan tidak terdistribusi jika term itu ditujukan kepada sebagian saja dari anggota kelas yang berkedudukan sebagai term tersebut di dalam proposisi yang bersangkutan (luas cakupan/sebaran)

Ragaan/Diagram Distribusi Term

Latihan 5

1. Sebagian orang bekerja dengan tidak-rajin.
2. ebagian orang tidak bekerja dengan rajin.
3. Lima dari seratus orang pengemudi kendaraan bermotor pernah mengalami kecelakaan lalu lintas.
4. Masih banyak penduduk mendapat perlakuan tidak-adil.
5. Hampir semua yang rajin bekerja hampir mendapat hasil banyak.
6. Tidak ada kucing makan rumput
7. Tidak satu pun gajah makan daging.
8. Tidak semua burung bisa terbang.
9. Masyarakat Indonesia mau tidak-mau harus waspada terhadap wabah demam berdarah.
10. Setiap pejabat negara menjunjung tinggi moralitas.

Macam Proposisi bedasarkan Kompleksitas

• Proposisi Sederhana (simple proposition) adalah proposisi yang memiliki satu subjek dan satu predikat.
• Proposisi Majemuk (compound proposition) adalah proposisi yang tersusun atas dua atau lebih proposisi sederhana.

Proposisi-proposisi sederhana yang mewujudkan sebuah proposisi majemuk disebut Proposisi Komponen. Proposisi majemuk dibedakan dalam 2 jenis yakni Proposisi Kompositif dan Proposisi Konjungtif.

Proposisi Kompositif terdiri atas:

• Proposisi Hipotetikal,
• Proposisi Alternatif
• Proposisi Disjungtif
• Proposisi Konjungtif.

Proposisi Hipotetikal

Proposisi hipotetis adalah proposisi yang terdiri atas bagian-bagian yang satu sama lainnya (satu premis atau lebih) memiliki hubungan yang bersifat saling bergantung, bertentangan atau memiliki kesamaan.

Jika….(proposisi antesenden/sebab)…., maka….(proposisi konsekuen/akibat)…..

If………, then….

Konsekuennya benar, belum tentu antesendennya benar. Bila antesendennya benar, konsekuennya pasti benar.

Jika hujan, aku tidak pergi.

Antecendensnya adalah jika hujan, Konsequesinya adalah adalah aku tidak pergi.

Jika antecendensnya disebut A, dan konsequensinya B, akan terjadilan yang berikut ini:

• Jika A benar, B juga benar
• Jika B salah, A juga salah
• Jika A salah, B dapat salah tetapi juga dapat benar
• Jika B benar, A dapat salah tetapi juga dapat benar

Latihan 6

Tentukan antecendensnya dan konsequensinya !

Jika liontin yang dikenakan itu terbuat dari berlian, maka harganya sangat mahal



Proposisi Alternatif/Alternan

Proposisi alternatif adalah proposisi majemuk yang terdiri dari dua proposisi komponen dan salah satu dari proposisi komponennya adalah benar atau dua-dunya benar (sekurang-kurangnya satu proposisi benar.)

Atau…., atau……….

Either….., or…..

Proposisi alterntif dapat diubah/dikonversi menjadi proposisi hipotetikal dengan menegasi salah satu alternannya.

Jika….., maka…(tidak)….

Contoh :

• Atau dosen mengajar, atau mahasiswa malas ikut kuliah
• Atau membatalkan pembangunan kereta cepat, atau rakyat akan demonstrasi
• Atau gaya kepemimpinan yang transformatif, atau motivasi karyawan yang rendah

Proposisi Disjungtif

Proposisi disjungtif adalah proposisi majemuk yang terdiri atas dua proposisi komponen yang kedua-duanya salah.

Tidak demikian halnya bahwa,….dan….

Adalah tidak benar, bahwa…..dan….

Neither…., nor….

Proposisi Konjungtif

Proposisi konjungtif adalah proposisi majemuk yang proposisi-proposisi komponennya sama derajatnya sehingga masing-masing dapat dikemukakan yang satu lepas dari yang lain tanpa mengubah maksudnya.

…., dan…..

Contoh:

• Pak Yusuf adalah dosen, dan Jessica adalah seorang mahasiswa
• Pendidikan harus mengedepankan kualitas, dan ekonomi menitikberatkan pada pemerataan pembangunan.

HUBUNGAN ANTAR PROPOSISI

Proposisi AEIO dapat dihubungkan satu sama lain untuk menguji pernyataan.

Caranya:

• Mengandaikan pernyataan benar, atau mengandaikan pernyataan salah atau nilai kebenaran pernyataan yang satu menentukan nilai pernyataan lainnya.
• Subjek dan predikatnya harus sama
• Tidak harus tahu faktanya lebih dahulu.
• Pengujian ini berupa pengandaian!
• Jangan disangkutpautkan dengan faktanya.
• Jika perlu digunakan, fakta akan dijadikan patokan.

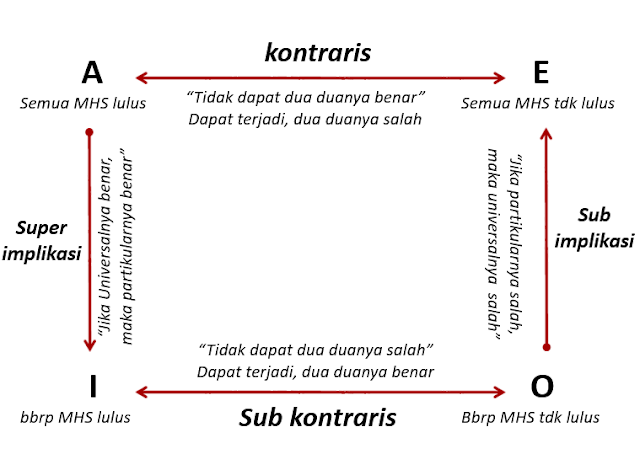
MACAM-MACAM HUBUNGAN ANTAR PROPOSISI

HUBUNGAN EKUIVALENSI / KO-IMPLIKASI

Hubungan 2 proposisi yang sama, sedemikian rupa sehingga jika yang satu benar maka yang lain benar; demikian pula sebaliknya.

Pola: P = Q (≠ Proposisi hipotetikal…Jika P maka Q )

Contoh: 

“Semua hewan abadi” berhubungan ekuivalensi dengan “Semua hewan tidak tak-abadi” (non-abadi)

• Jika P benar maka Q benar.
• Jika P salah maka Q salah.
• Jika Q benar maka P benar.
• Jika Q salah maka P salah.

HUBUNGAN BEBAS

Hubungan 2 proposisi, satu proposisi tidak mengimplikasikan proposisi lain. Hubungan bebas = proposisi konjungtif (…..dan…..)

Pola: A dan B

Contoh: 

Anita menari (A) dan Budi bermain musik (B).

Proposisi A tidak mempengaruhi nilai kebenaran dari proposisi B; demikian pula sebaliknya.

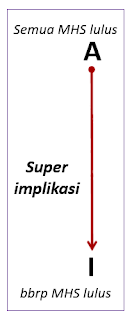
HUBUNGAN SUPER-IMPLIKASI

Hubungan antara dua proposisi (A ke I dan E ke O) yang dimana:

• Kuantifiernya berbeda: dari proposisi universal ke proposisi partikular kopulanya sama yakni sama-sama positif atau sama-sama negatif
• Superimplikasi: hubungan proposisi A dengan I atau E dengan O.

• Jika A (E) benar maka I (O) benar.
• Jika A (E) salah maka I (O) tidak dapat dipastikan benar-salahnya.

“Jika Universalnya benar, maka partikularnya BENAR”

KETERANGAN

• Jika proposisi A benar, maka proposisi I PASTILAH benar
• Jika semua MHS lulus (benar: sesuai kenyataan), maka pernyataan “beberapa MHS lulus” PASTILAH benar (benar: sesuai kenyataan).
• Jika Proposisi A salah, maka proposisi I bisa benar dan bisa salah.
• Jika “semua MHS lulus” (tidak sesuai kenyataan/salah), maka kenyataannya adalah 1) bisa jadi, hanya “beberapa MHS lulus”, atau 2. bisa juga, “semua MHS tidak lulus” (artinya pernyataan “beberapa MHS lulus” ditarik dari proposisi universalnya “semua MHS lulus”.)
• Jika proposisi A tidak sesuai kenyataan (tidak benar), maka proposisi I bisa benar (“bbrp MHS lulus”), tetapi bisa juga tidak benar karena yang benar adalah “ semua MHS tidak lulus”.

HUBUNGAN SUB-IMPLIKASI

Hubungan antara dua proposisi (I ke A dan O ke E) yang dimana:

• Kuantifiernya berbeda: dari proposisi partikular ke proposisi universal (sub-implikasi)
• Kopulanya sama: Sama-sama positif atau sama-sama negatif
• Sub implikasi: hubungan proposisi I dengan A atau O dengan E

• Jika I (O) benar maka A (E) tidak dapat dipastikan benar-salahnya.
• Jika I (O) salah maka A (E) salah

“Jika partikularnya salah, maka universalnya pun salah”


KETERANGAN

• Jika proposisi I tidak benar, maka proposisi A PASTILAH tidak benar
• Jika beberapa MHS lulus (tidak benar: tidak sesuai kenyataan), maka pernyataan “semua MHS lulus” PASTILAH salah (tidak sesuai kenyataan).
• Jika Proposisi I benar, maka proposisi A bisa benar dan bisa salah.
• Jika “beberapa MHS lulus” (sesuai kenyataan), maka kenyataan lainnya adalah 1) bisa jadi, “beberapa MHS tidak lulus”, atau 2. bisa juga, “semua MHS lulus” (artinya pernyataan “beberapa MHS lulus” ditarik dari proposisi universalnya “semua MHS lulus”.)
• Jika proposisi I sesuai kenyataan (benar), maka proposisi A bisa benar (“semua MHS lulus”), tetapi bisa juga tidak benar karena yang benar adalah “beberapa MHS tidak lulus”.

HUBUNGAN KONTRARIS

Hubungan antara dua proposisi (A ke E atau E ke A) yang dimana:

• Kuantifiernya sama-sama universal (luas S Universal)
• Kopulanya berbeda:
• •Yang satu positif, yang lainnya negatif
• •Antara proposisi A dengan proposisi E.

• Tidak mungkin kedua-duanya benar
• Karena kopula A: positif, dan E: negatif
• Jika proposisi A dianggap benar, maka proposisi E dianggap Salah
• Jika proposisi E dianggap benar, maka proposisi A dianggap Salah

• Dapat terjadi kedua proposisi ini sama-sama salah
• Karena luas S proposisi A dan E sama-sama universal
• Jika proposisi A dianggap salah, maka E tidak dapat dipastikan benar/salah.
• Jika proposisi E dianggap salah, maka A tidak dapat dipastikan benar/salah

KETERANGAN

• Jika proposisi A benar, maka proposisi E PASTI salah.
• Jika Semua MHS lulus (benar: sesuai kenyataan), maka pernyataan “Semua MHS tidak lulus” PASTILAH salah (tidak benar: tidak sesuai kenyataan).
• Jika Proposisi A salah, maka proposisi E bisa benar dan bisa salah.
• Jika “semua MHS lulus” (tidak sesuai kenyataan), maka kenyataannya adalah 1. bisa jadi, “Semua MHS tidak lulus”, atau 2. bisa juga, “Beberapa MHS lulus”.
• Jika proposisi A tidak sesuai kenyataan (tidak benar), maka proposisi E bisa benar (“Semua MHS tidak lulus”), tetapi bisa juga salah karena yang benar adalah “Beberapa MHS lulus”.

HUBUNGAN SUB-KONTRARIS

Hubungan antara dua proposisi (I ke O atau O ke I) yang dimana

• Kuantifiernya sama-sama partikular
• Kopulanya berbeda: yang satu positif (I) dan lainnya negatif (O).
• Hubungan antar proposisi partikular positif (I) dengan partikular negatif (O

Kedua proposisi tersebut dapat dianggap sama-sama benar.

• Karena luas S proposisi I dan O sama-sama partikular
• Jika proposisi I dianggap benar, proposisi O juga dianggap benar.
• Jika proposisi O dianggap benar, proposisi I juga dianggap benar

Kedua proposisi ini tidak mungkin sama-sama salah

• Karena kopula I positif dan kopula O negatif
• Jika yang satu salah, yang lain harus benar
• Jika proposisi I salah, maka O harus benar
• Jika proposisi O salah, maka proposisi I benar
• Jika proposisi I benar, maka proposisi O tidak dpat dipastikan benar /salah
• Jika proposisi O benar, maka proposisi I tidak dpat dipastikan benar /salah

KETERANGAN

• Jika proposisi I salah, maka proposisi O PASTI benar
• Jika beberapa MHS lulus (salah: tidak sesuai kenyataan), maka pernyataan “beberapa MHS tidak lulus” PASTILAH benar (benar: sesuai kenyataan).
• Jika Proposisi I benar, maka proposisi O bisa benar dan bisa salah.
• Jika “beberapa MHS lulus” (sesuai kenyataan), maka kenyataannya adalah 1) bisa jadi, “beberapa MHS tidak lulus”, atau 2. bisa juga, “semua MHS lulus” (artinya pernyataan “beberapa MHS lulus” ditarik dari proposisi universalnya “semua MHS lulus”.)
• Jika proposisi I sesuai kenyataan (benar), maka proposisi O bisa benar (“bbrp MHS tidak lulus”), tetapi bisa juga tidak benar karena yang benar adalah “ semua MHS lulus”.

HUBUNGAN KONTRADIKSI

• Dua proposisi yang kuantifiernya berbeda (kuantitas) dan kopula berbeda (kualitas)
• Universal positif (A) dengan partikular negatif (O) (A ke O atau O ke A dan E ke I atau I ke E)
• Tidak mungkin kedua proposisi itu dianggap benar:
• Jika yang satu dianggap benar maka yang lain dianggap salah
• Tidak mungkin kedua proposisi itu dianggap salah
• Jika yang satu dianggap salah maka yang lain dianggap benar
• Jika A (E) benar maka O (I) salah
• Jika A (E) salah maka O (I) benar
• Jika O (I) benar maka A (E) salah
• Jika O (I) salah maka A (E) benar

GAMBAR HUBUNGAN ANTAR PROPOSISI

CARA MUDAH MENENTUKAN TINGKAT KEBENARAN HUBUNGAN PROPOSISI

KESIMPULAN

Jika Prop Universal BENAR, maka semua proposisi mempunyai kepastian nilai kebenaran


Jika A benar, I benar, E & O salah
Jika E benar, O benar, A & I salah

Jika Prop Partikular SALAH, maka semua proposisi mempunyai kepastian nilai kebenaran.


Jika I salah, A salah, E & O benar
Jika O salah, E salah, A & I benar

Jika Prop Universal SALAH, maka hanya satu yang punya kepastian nilai kebenaran, yaitu kontradiksinya dan berlawanan nilainya.

Jika A salah, O benar, E dan I TDD
Jika E salah, I benar, A dan O TDD



Jika Prop Partikular BENAR, maka hanya satu yang punya kepastian nilai kebenaran, yaitu kontradiksinya dan berlawanan nilainya


Jika I Benar, E salah, A dan O TDD
Jika O benar, A salah, E dan I TDD.