Struktur Diskrit : Konektivitas, Path, dan Circuit
Paths
A path of length n is a sequence of n edges that begins at a vertex of a graph and travels from vertex to vertex along edges of the graph.
Let n be a nonnegative integer and G an undirected graph. A path of length n from u to v in G is a sequence of n edges e1,...,en of G for which there exists a sequence x0 = u,x1,...,xn−1,xn =v of vertices such that ei has, for i =1,...,n, the endpoints xi-1 and xi
The path is a circuit (or cycle) if it begins and ends at the same vertex. A path or a circuit is simple if it does not contain the same edge more than once.
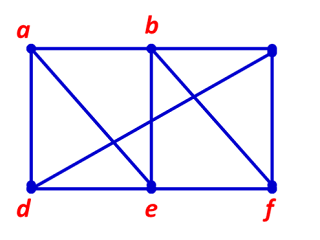
Example
- a, d, c, f, e is a path
- d, e, c, a is a not a path
- b, c, f, e, b is a circuit
- a, b, e, d, a, b is not a simple path
Paths in Acquaintanceship Graphs
There is a path between two people if there is a chain of people linking these people, where two people adjacent in the chain know one another.
There is a chain of six people linking Kamini and Ching.
Paths in Collaboration Graphs
There is a path between two people if there is a chain of people linking these people, where two people adjacent in the chain know one another.
Academic collaboration graph
Two people a and b are connected by a path when there is a sequence of people starting with a and ending with b such that the endpoints of each edge in the path are people who have collaborated.
The Erd˝os number of a mathematician is the length of the shortest chain of mathematicians that begins with Paul Erd˝os and ends with this mathematician, where each adjacent pair of mathematicians have written a joint paper.
Hollywood graph
Two actors a and b are linked when there is a chain of actors linking a and b, where every two actors adjacent in the chain have acted in the same movie.
The Bacon number of an actor c is defined to be the length of the shortest path connecting c and the well-known actor Kevin Bacon.
Connectedness in Undirected Graphs
An undirected graph is called connected if there is a path between every pair of distinct vertices of the graph.
Connected Component
A connected component of a graph G is a connected subgraph of G that is not a proper subgraph of another connected subgraph of G.
A connected component of a graph G is a maximal connected subgraph of G.
A graph G that is not connected has two or more connected components that are disjoint and have G as their union.
Cut Vertices and Cut Edges
A vertex is a cut vertex (articulation point) when the removal of this vertex produces a subgraph that is not connected. An Edge is a cut edge (bridge) when the removal of this edge produces a subgraph that is not connected.
The cut vertices of G are b, c, and e. The edges of G are (a,b) and (c,e).
Connectedness in Directed Graph
A directed graph is strongly connected if there is a path from a to b and from b to a whenever a and b are vertices in the graph.
A directed graph is weakly connected if there is a path between every two vertices in the underlying undirected graph (when the direction is disregarded).
Example :
Strongly Connected Components
A strongly connected components or strong component of G is the subgraphs of a directed graph G that are strongly connected by not contained in larger strongly connected subgraphs, that is , the maximal strongly connected subgraphs.
Example :
- Graph H has three strongly connected components:
- Vertex a
- Vertex e
- Vertices b, c, d
Path and Isomorphism
Graphs, G1 and G2 are isomorphism only if in both graph exist a simple circuit of same length k (k >2).
Example :
- Graph G and H, both have 6 vertices and 8 edges.
- Each has 4 vertices of degree three, and two vertices of degree two.
- H has a simple circuit of size three but all simple circuits in G have length at least four. So, G and H are not isomorphic.
Counting Paths between Vertices
Let G be a graph with adjacency matrix A with respect to the ordering v1, v2, …, vn (with directed or undirected edges, with multiple edges or loops allowed).
The number of different paths of length r from vi to vj, where r is a positive integer, equals the (i, j)th entry of Ar .
Exercise
How many paths of length 4 are there from a to d in G ?
Hence, there are 8 paths of length 4 from a to d.
Sumber
Slide Strukdis : Circuit and Path















Posting Komentar