Algoritma dan Struktur Data : Sorting Dasar dan Contoh Soal
Definition
Sorting is the process of rearranging a sequence of objects and put them in some logical order. For this problem to be meaningful, the nature of the list items must allow such an ordering.
Computational problem :
- Input : A sequence of n numbers {A1, A2, A3, . . . , An}
- Output : A permutation (reordering) {A′1, A′2, A′3, . . . , A′n } of the input sequence such that A′1 ≤ A′2 ≤ A′3 ≤. . . ≤ A′n
Example :
In practice, not only numbers: characters, strings, collection of data (records) containing a key to be sorted or any other ordered types.
Motivation
It’s one of the most fundamental algorithmic problem in computer science :
- As the starting point to solve other problems and basic building block for many other algorithms (ex: Greedy, Searching)
- Design of algorithms similar in sorting are effective in addressing other problems, ex: divide-and-conquer
- Historically, computers spent more time to sort than doing anything else.
- Literally dozens of different algorithms are known, most of which possess some particular advantage over all other algorithms in certain situations.
- It plays a major role in commercial data processing and in modern scientific computing.
Sorting Characteristics
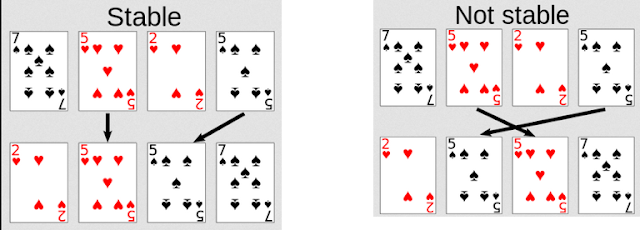
Stable
Preserves the relative order of any two equal elements in its input. If an input list contains two equal elements in positions i and j where i < j, then in the sorted list they have to be in positions i’ and j’ respectively, such that i’ < j’.
In-place
In-place: does not require extra memory, except, possibly, for a few memory units.
Internal-External
Whether there are so many records to be sorted that they must be kept in external files (on disks, tapes, etc) or whether they can all be kept internally in high-speed memory.
Comparison-Based
Comparison-based sorting works by comparing elements to be sorted. Non-comparison based sorting: radix sort, bucket sort, count sort, etc.
Types of Sorting Algorithms
Pragmatics of Sorting
Increasing or decreasing order ?
Sorting just the key or an entire record ?
Equal keys ?
Non-numerical data ?
Running Time
Running time for Sorting Algorithms usually depends on the number of
Which one is more important? Data comparison or data movement? What if the data is large?
Time Case
Best case: data is already sorted
Worst case: data is reversely sorted
Average case: data is not sorted (the order is random)
Basic Sorting
Selection Sort
Idea
Works by selecting an element and move it to its proper position. Assume we have an array of n integers with random order:
- Find the smallest elements in the array
- Exchange the smallest elements with the first element in the array
- Starting from the second element, find the smallest element among the last n-1 elements
- Exchange it with the second element in the array
- Continue until only one element remain unsorted
Illustration
Pseudocode
Running Time
Insertion Sort
Idea
Works by inserting an element into its proper position in already sorted (sub)-array. Assume we have an array of n integers with random order:
- The first element in already sorted
- Insert the second element into already sorted sub-array contains the first element
- Now sub-array contains two elements is already sorted
- Repeat the process with the next (unsorted) element. The size of a sorted sub-array is growing.
- Continue until the last element is inserted and the array is sorted
Illustration
Pseudocode
Running Time
Shell Sort
Idea
ShellSort is an upgrade over Insertion Sort (It was created by Donald L. Shell in 1959).
- Selection Sort: moves element efficiently, but does many redundant comparison
- Insertion Sort: minimum number comparison (at average), but inefficient by moving element one position at a time
ShellSort (Diminishing-increment Sort) is an extension of insertion sort, it allows exchanging array elements that are far apart. It divides the array into several sub-arrays containing elements far apart (not contiguous but every h-th element, h is gap between elements). Sort each of sub-arrays, eventually move small elements relatively in front of others. Repeated (with decreasing value of h) and it will produce partially sorted arrays that can be efficiently sorted, eventually by Insertion Sort
Illustration
Assume we have an array of n integers with random order. The values of h used is 4, 3 and 1.
The first sub-array {21, -123} with h = 4 is sorted.
The second sub-array with h = 4 is sorted
The third sub-array with h = 4 is sorted
The fourth sub-array with h = 4 is sorted
Continue with h = 3. The first sub-array {-123,62} with h = 3 is sorted
The second sub-array with h = 3 is sorted
The third sub-array with h = 3 is sorted
Finally, sort it with h = 1
Pseudocode
Running Time
Best Case: θ(n)
Worst Case: θ(n^2) (Shell,1959), O(n^(4/3)) (Sedgewick,1986)
Sorting in JDK
Sorting primitive types: Java provides Arrays.sort. It uses TimSort, which is a divide and conquer algorithm.
Example :
import java.util.Arrays;
1. int[] A= {7,5,61,4,2};
2. Arrays.sort(A);
3. //prints 2, 4, 5, 7, 61
4. System.our.println(Arrays.toString(A));
Sorting in JDK: Objects
Implements comparable and override method compareTo()
Exercise
- Sort {7, 6, 5, 4, 3, 2, 1} non-increasingly using Selection Sort and Insertion Sort. Show the steps !
- Which algorithm is better to sort {7,6,5,4,3,2,1} non-decreasingly ? Selection Sort or Insertion Sort ? Why ?
- Which algorithm is better to sort {7,6,5,4,3,2,1} non-increasingly ? Selection Sort or Insertion Sort ? Why ?
Sumber
Slide ASD : Sorting Dasar






























Posting Komentar