Logika Informatika : Sifat Kalimat, Pohon Semantik, dan Pengujian 2 Kalimat, beserta Contoh Soal

Pengantar Informatika : Sistem Bilangan, Biner, Desimal, Oktal, Heksadesimal, dan Contoh Soal

Komputer & Data

Komputer menggunakan konsep sistem dijital dalam mengkomunikasikan data/informasi. Sebagai perangkat elektronik, komputer hanya mengenal status On atau status Off.

Bilangan 1 digunakan untuk merepresentasikan status On dan Bilangan 0 untuk status Off. Semua data ( serumit apapun ) harus direpresentasikan di dalam memori dalam bentuk dijit biner ( bits = binary digits ). Representasi dalam bentuk dijit biner, tidak mudah dipahami, sehingga digunakan sistem bilangan oktal dan hexadesimal sebagai perantara untuk memahami penempatan data di dalam komputer.

Contoh I

Representasi data di dalam komputer

Contoh II

PL Algoritma Rabin

1. Program Enkripsi–Dekripsi file data
2. File berbagai tipe (txt, bmp, jpg, doc, xls, wma, ppt, java, rar, pdf) menjalani proses enkripsi (disandikan) agar tidak mudah dibuka.
3. File yang akan dienkripsi, ditampilkan dalam kode hexadesimal agar mudah diperiksa.
4. Proses enkripsi membutuhkan kunci privat dan kunci publik
5. File hasil enkripsi ditampilkan juga dalam kode hexadesimal.

Sistem Bilangan

1. Ada beberapa sistem bilangan yang digunakan dalam sistem digital. 
2. Yang umum digunakan adalah sistem bilangan desimal, biner, oktal, dan heksadesimal
3. Sistem bilangan desimal merupakan sistem bilangan yang paling familiar karena dipergunakan sehari – hari.

Desimal (Basis/Radiks-10)

Sistem Bilangan yang paling umum digunakan dalam kehidupan sehari-hari.

Deca artinya 10.

• Menggunakan 10 macam simbol bilangan yaitu : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Dapat berupa integer desimal (decimal integer) dan dapat juga berupa pecahan desimal (decimal fraction)

Setiap simbol dalam sistem bilangan desimal memiliki Absolut Value dan Position Value

• Absolut value adalah Nilai Mutlak dari masing-masing digit bilangan
• Position Value adalah Nilai Penimbang atau bobot dari masing- masing digit bilangan tergantung dari letak posisinya yaitu bernilai basis dipangkatkan dengan urutan posisinya

Bilangan desimal 8598 dapat diartikan : 

Sistem bilangan desimal dapat berupa pecahan desimal (decimal fraction)

• Untuk bilangan integer posisi digit dimulai dari sebelah kanan
• Untuk bilangan pecahan posisi digit dimulai dari sebelah kiri

Bilangan Pecahan Desimal (decimal fraction)

Biner ( Basis / Radiks-2)

Terdiri dari 2 simbol : 0 dan 1. Dipopulerkan oleh John Von Neumann

Contoh :

Position Value dalam sistem Bilangan Biner merupakan perpangkatan dari nilai 2 (basis), seperti pada tabel

Contoh :

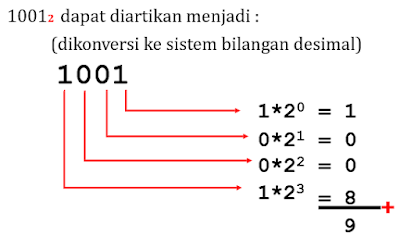
Konversi Bilangan Desimal ke Biner

1. Bilangan desimal (D10) dibagi 2 (nilai pembagi=2).
2. Setiap data sisa pembagian disebut Least Significant Bit (LSB)
3. Lakukan terus menerus (suksesif) sampai hasil baginya = 0 (nol)
4. Data sisa pembagian yang terakhir menjadi Most Significant Bit (MSB)
5. Susun data LSB mulai dari data MSB dilanjutkan dengan data LSB terbawah sd data LSB teratas
6. Terbentuk (D2) sebagai bilangan biner

Latihan 1

Oktal ( Basis / Radiks-8 )

Terdiri dari 8 simbol : 0, 1, 2, 3, 4, 5, 6, 7

Contoh :

Position Value dalam Sistem Bilangan Oktal merupakan perpangkatan dari nilai 8 (basis 8)

Contoh :

Heksadesimal ( Basis / Radiks-16 )

Hexa berarti 6 dan Desimal berarti 10

Terdiri dari 16 simbol 

• 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 
• A(10), B(11), C(12), D(13), E(14), F(15) 

Memadukan 2 unsur yaitu angka dan huruf. 

• Huruf A mewakili angka 10 
• Huruf B mewakili angka 11 dan seterusnya sampai huruf F mewakili angka 15

Contoh :

Position Value dalam Sistem Bilangan Hexadesimal merupakan perpangkatan dari nilai 16 (basis)

Contoh :

Konversi Basis-r ke Desimal

Konversi Bilangan Desimal ke Oktal

1. Bilangan desimal (D10) dibagi 8 (nilai pembagi=8)
2. Setiap data sisa pembagian disebut Least Significant Bit (LSB)
3. Lakukan terus menerus (suksesif) sampai hasil baginya = 0 (nol)
4. Data sisa pembagian yang terakhir menjadi Most Significant Bit (MSB)
5. Susun data LSB mulai dari data MSB dilanjutkan dengan data LSB terbawah sd data LSB teratas
6. Terbentuk (D8) sebagai bilangan Oktal

Konversi Bilangan Desimal ke Hexadesimal

1. Bilangan desimal (D10) dibagi 16 (nilai pembagi=16)
2. Setiap data sisa pembagian disebut Least Significant Bit (LSB)
3. Lakukan terus menerus (suksesif) sampai hasil baginya = 0 (nol)
4. Data sisa pembagian yang terakhir menjadi Most Significant Bit (MSB)
5. Susun data LSB mulai dari data MSB dilanjutkan dengan data LSB terbawah sd data LSB teratas
6. Terbentuk (D16) sebagai bilangan Hexadesimal

Konversi Bilangan Biner ke Oktal

Untuk mengkonversi bilangan biner ke bilangan oktal : Lakukan pengelompokan 3 dijit bilangan biner dari posisi LSB sampai ke MSB

Artinya : pengelompokan dimulai dari 3 dijit terakhir dan seterusnya hingga seluruh dijit dalam bilangan biner selesai dikelompokan

Konversi Bilangan Oktal ke Biner

Sebaliknya untuk mengkonversi Bilangan Oktal ke Biner yang harus dilakukan adalah :

Terjemahkan setiap dijit bilangan oktal ke 3 dijit bilangan biner

Konversi Bilangan Biner ke Hexadesimal

Untuk mengkonversi bilangan biner ke bilangan hexadesimal :

Lakukan pengelompokan 4 dijit bilangan biner dari posisi LSB sampai ke MSB

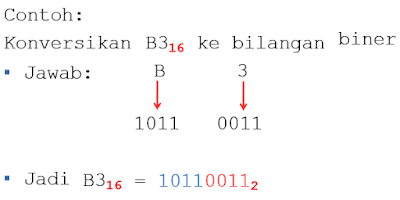
Konversi Bilangan Hexadesimal ke Biner

Sebaliknya untuk mengkonversi Bilangan Hexadesimal ke Biner yang harus dilakukan adalah :

Terjemahkan setiap dijit bilangan Hexadesimal ke 4 dijit bilangan biner

Latihan 2

Jawaban Latihan 2

Operasi Penjumlahan Bilangan Biner

Operasi penjumlahan pada sistem bilangan biner dilakukan sama seperti operasi penjumlahan pada sistem bilangan desimal

Aturan penjumlahan pada bilangan biner :

Latihan 3

Operasi Pengurangan Bilangan Biner

Operasi pengurangan pada sistem bilangan biner dilakukan sama seperti operasi pengurangan pada sistem bilangan desimal.

Aturan operasi pengurangan pada sistem bilangan biner :

Latihan 4

Operasi Perkalian Bilangan Biner

Operasi perkalian pada sistem bilangan biner dilakukan sama seperti operasi perkalian pada sistem bilangan desimal.

Aturan operasi perkalian pada sistem bilangan biner :

Contoh :

Dua keadaan dalam perkalian sistem bilangan biner : 

• Jika pengali adalah bilangan 1, maka cukup disalin saja 
• Jika pengali adalah bilangan 0, maka hasilnya semuanya 0

Operasi Pembagian Bilangan Biner

Operasi pembagian pada sistem bilangan biner dilakukan sama seperti operasi pembagian pada sistem bilangan desimal.

Operasi pembagian dengan 0 tidak mempunyai arti.

Aturan operasi pembagian pada sistem bilangan biner :

Contoh :

Latihan 5