Pengantar Logika : Kerancuan Berpikir dan Jenisnya

Matematika Dasar : Persamaan Garis Lurus dan Contoh Soal

Bentuk umum

y=mx+c; m,c ∈ R 

ax+by+c=0; a,b,c∈R 

Contoh

y=3x+4

y=2x+2

2x+3y=12 

Persamaan Gris Lurus juga bisa disebut dengan persamaan linear dimana bersifat geometris berupa garis yang lurus.

Menggambar Grafik Persamaan Garis Lurus

1. Ambil 2 buah titik sembarang 
2. Tarik garis yang melalui kedua garis tersebut 

Contoh

2x+3y=12

PGL dengan persamaan 2x+3y=12

Latihan 1

Gambarlah grafik berikut ini !

1. y=x+2 
2. y=2x+4 
3. y=-3x+1 
4. x+2y=4 
5. 3x-2y=6

Menentukan Persamaan Garis Lurus

1. Ambil dua buah titik 
2. Masukkan ke bentuk umum persamaan garis 
3. Selesaikan dua buah persamaan yang terbentuk

Gradien

Gradien adalah tingkat kemiringan suatu garis tertentu.

Bentuk Umum Gradien

m = Δy / Δx
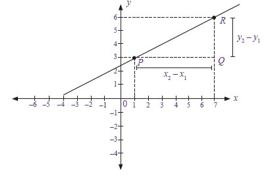
m = ( y2-y1 )/( x2-x1 )

Dari rumus y=mx+c didapatlahm. m disini adalah gradien yang berasal dari turunan rumus PGL. Apabila mengintegralkan gradien, maka didapatkan persamaan baku PGL.

Latihan 2

Tentukanlah gradien garis dari persamaan berikut !

1. 2x+3y=12
2. 5x-2y=18
3. -y=2x+3
4. Tentukan persamaan garis yang melalui titik (3,11) dan memiliki gradien 2!

Gradien garis yang saling sejajar

Merupakan Dua buah garis yang sejajar memiliki gradien yang sama 

Bentuk Umum

Jika L1//L2, maka m_1=m_2 

Latihan 3

1. y=2x+4 dan y=2x-3 
2. 6x+2y=3 dan y=7-3x

Gradien garis yang saling tegak lurus

Merupakan Dua buah garis yang tegak lurus memiliki gradien yang berkebalikan dan berlawanan .

Bentuk Umum

Jika L1 ⊥ L2, maka m1=-1/m2 atau m1⋅m2=-1 

Latihan 4

1. y=2x+4 dan y=-1/2 x-3 
2. 2x-6y=3 dan y=7-3x

Membuat Persamaan Garis

Bentuk Umum ( Cara cepat )

(y-y1)/(y2-y1 ) = (x-x1) / (x2-x1 ) 

Latihan 5

Tentukan persamaan garis yang melalui

1. (2,1) dan (-1,3) 
2. (2,4) dan (5,1) 
3. (1,0) dan (1,-4) 
4. (-3,-1) dan (2,-1)

Persamaan Garis yang Sejajar Garis Lain

Persamaan garis yang melalui titik (x1, y1) dan sejajar garis y = mx + c adalah:

y – y1 = m(x – x1)

Cara Cepat

Diketahui Titik dan PGL yang sejajar

ax±by=a.x1 + b.y1

Latihan 6

1.Tentukan persamaan garis yang sejajar dengan garis 2x-4y=5 dan melalui titik (1,0)! 

2.Tentukan persamaan garis yang sejajar dengan garis y=4-x dan melalui titik (5,1)!

Persamaan Garis yang Tegak Lurus Garis Lain

persamaan garis yang melalui titik (x1, y1) dan tegak lurus dengan garis y = mx + c adalah:
y – y1 = (–1/m)(x – x1)

Latihan 7

1.Tentukan persamaan garis yang tegak lurus dengan garis 2x-4y=5 dan melalui titik (1,0)! 

2.Tentukan persamaan garis yang tegak lurus dengan garis y=4-x dan melalui titik (5,1)!

Titik dan Garis

Jarak Dua Buah Titik

Rumus untuk menentukan Jarak titik (x1,y1) dan (x2,y2 ) adalah: 

√((x_2-x_1 )^2+(y_2-y_1 )^2 ) 

Latihan 8

Tentukan jarak dua buah titik berikut !

1.(2,-1) dan (-1,3) 

2.(2,4) dan (5,1) 

3.(1,0) dan (1,-4) 

4.(-3,-1) dan (2,-1) 

Hubungan Titik dan Garis

Apabila garis L1 dan L2 tidak sejajar, maka garis L1 pasti memotong L2 di sebuah titik ! 

Latihan 9

Tentukan titik perpotongan kedua garis berikut (jika ada) ! 

1. y=2x+1 dan y=-3x+6 
2. 2x+3y=3 dan 5x-y-2=0 
3. 4x-y-1=2 dan 8x=2y+2

Jika titik P(x1,y1) tidak berada di garis L1 : ax+by+c=0, maka jarak P ke L1 pasti lebih dari 0. 

Latihan 10

Tentukan jarak dari titik (3,2) ke garis 4x+3y+7=0 

Cara cepat mencari jarak titik ke garis atau garis dengan garis

d = |ax1+by1+c| / √(a^2+b^2) 

Catatan

• Jarak garis ke titik atau garis ke garis harus tegak lurus !
• Untuk garis ke garis, carilah terlebih dahulu titik pada satu garis yang sejajar dengan garis tersebut

Latihan 11

Tentukan jarak dari garis y=x+3 dan 2y-2x+5=0! 

Latihan 12

1. Tentukan jarak antara pasangan titik-titik berikut: 
• P (3 , 7) dan Q (5 , -4). 
• A (-2 , -2) dan C (1 , 5). 
2. Tentukan suatu persamaan lingkaran : 
• yang melalui tiga titik A (4 , 5), B (3 , -2) dan C (1 , -4). 
• yang berpusat di (-2 , 5) dan menyinggung garis x = 7. 
• yang menyinggung garis 3𝑥 + 𝑦 − 5 = 0 di (-1 , 1) dan melalui titik (3 , 5). 
3. Tentukan persamaan-persamaan garis lurus berikut: 
• melalui titik (5, -5) dengan kemiringan 1,4. 
• m elalui titik (4,2) dan (-3,-4). 
• Dengan intersep-y 3 dan kemiringan 2. 
4. Carilah kemiringan dan intersep-y untuk tiap garis: 
• 3y = -2x+1 
• -4y = 5x-6 
5. Diketahui garis l dengan persamaan 2𝑦 − 3𝑥 = 4 dan titik P ( 1 , -3). Tentukan suatu persamaan garis yg melalui P dan tegak lurus l
6. Tentukan persamaan garis yang melalui titik (2,3) sejajar 2x + 5y - 1 = 0 adalah.......
7. Tentukan persamaan garis yang melaui titik (1,4) sejajar dengan 3x + 2y - 5 = 0 adalah........
8. Jika titik (a, b) terletak pada garis 3x – 2y – 6 = 0 dan terdekat dengan titik (4, 3), maka b – a =...
9. Persamaan garis lurus yang berpotongan dan tegak lurus dengan garis ax + 2y + 7 = 0 di titik (3, 1) adalah...
10. Jika titik P(-3, 2), Q(6, 8), dan R adalah titik tengah PQ, maka persamaan garis yang tegak lurus dengan PQ dan melalui R adalah...
11. Titik potong antara garis y = ax – b dan y = cx + d, memiliki ordinat y =...
12. Jarak titik P(2, 3) ke garis 4x – 3y + 26 = 0 sama dengan jarak (5, m) ke titik P bila m sama dengan...
13. Garis yang melalui titik A(2, 8) dan B(-1, 2) dan garis yang melalui titik-titik C(0, 9) dan D(3, 0) akan berpotongan pada titik...