Pengantar Logika : Proposisi, Hubungan Antar Proposisi, Definisi Term, Sifat Term, dan Contoh Soal

Statistika : Data dengan Perhitungan Numerik, Rata-rata, Median, Modus, Kuartil, Interquartil Range, Boxplot, Five-Number Summary, dan Standar Deviasi

Pendahuluan

Grafik & Statistik

Adakah perbedaan untuk kedua kelas ?

Dari grafik → terlihat ada perbedaan

Seberapa signifikan ?

Grafik → tidak cukup untuk inferensi

Butuh ukuran statistik

Measures of Center

Ukuran Pusat

Dari 8 record: lihat “pusat” 

The Sample Mean

Mean : rata-rata 

Mean untuk sampel: x ̅ 

Mean untuk populasi: μ

Latihan 1

Berikut ini adalah data banyak anak dalam 10 keluarga :

2, 3, 0, 2, 1, 0, 3, 0, 1, 4 

Tentukanlah : 

• Sampel mean 
• Apa artinya ? 
• Misalkan terjadi kesalahan di mana keluarga terakhir terdata memiliki 40 anak (seharusnya 4 anak), Apa yang terjadi dengan mean? Data ekstrim (sangat besar atau sangat kecil): outlier

The Sample Median

Median: nilai tengah (data terurut)

Simbol: x ̃

Tujuan: mencari ukuran pusat sampel yang tidak terpengaruh oleh nilai ekstrim (outlier)

Ket :

• Banyak data: n
• Data terurut: x_1,x_2,…,x_n

Contoh : 

Tentukan median

1. 2, 3, 0, 2, 1, 0, 3, 0, 1, 4
2. 2, 3, 2, 1, 0, 3, 0, 1, 4

Latihan 2

Berikut ini adalah hasil dari 5 kali percobaan : 

1.7, 2.2, 3.9, 3.11, 14.7

Tentukan mean dan median ! 

Jawab: 

• Mean: x ̅=5.12 
• Median: x ̃=3.11 

Trimmed means

Mean yang diperoleh dengan membuang “sekian” persen nilai terbesar dan nilai terkecil

Contoh: 

2, 3, 0, 2, 1, 0, 3, 0, 1, 40 

Tentukan x ̅_(tr(10))!

x ̅_(tr(10)): buang data 10% terbesar 10% terkecil

Modus

Kategori yang paling banyak muncul 

Untuk variable kontinu yang dinyatakan dalam tabel frekuensi (atau frekuensi relatif): 

• Kelas dengan frekuensi tertinggi adalah modal class 
• Modus: nilai tengah dari modal class 

Bimodal: memiliki lebih dari satu modus

Contoh

Sampel hewan di padang rumput

Hewan yang paling banyak datang ke padang rumput ?

Tentukan modusnya !

Latihan 3

Berikut ini sampel pendapatan per tahun dari lima keluarga di lingkungan “Mawar” (dalam juta rupiah) : 

120, 120, 300, 90, 100

• Tentukan rata-rata pendapatan 
• Tentukan nilai tengah pendapatan 
• Tentukan pendapatan yang paling banyak muncul 
• Jika kamu ingin mempromosikan bahwa lingkungan “Mawar” adalah lingkungan yang makmur, ukuran mana yang akan kamu gunakan untuk mempresentasikan lingkungan “Mawar”? 
• Jika kamu ingin berargumen untuk melawan kenaikan pajak, ukuran apa yang akan kamu gunakan? 
• Jika kamu ingin mempresentasikan nilai tengah pendapatan, ukuran mana yang akan kamu gunakan?

Measures of Variability

Data rating hotel Bintang dan Bulan :

Bagaimanakah rating dari Bintang dan Bulan ?

Mean, median, modus kedua hotel sama

Apakah rating kedua hotel sama ?

Tidak!

Lihat persebaran data

Range

Range: perbedaan antara nilai terbesar dengan nilai terkecil

Range = x_max-x_min

Contoh

Hasil pengukuran terhadap nilai akhir kelas x di mata kuliah statistika:

Range = 99-20 =79

Latihan 4

Berikut ini adalah data banyak anak dalam 10 keluarga : 

2, 3, 0, 2, 1, 0, 3, 0, 1, 4

1. Tentukanlah range dari hasil pengukuran tersebut ! 
2. Misalkan terjadi kesalahan sehingga keluarga terakhir terdata salah yaitu memiliki 40 anak (seharusnya 4 anak), Apa yang terjadi dengan range ? 

Interquartil Range

Ukuran penyebaran yang mempertahankan ide dari range, tetapi tidak terpengaruh oleh nilai ekstrim

IQR: Mengukur persebaran dari 50% data yang berada di tengah

IQR = Q_3 - Q_1

Kuartil :

Membagi data menjadi 4 bagian

• Q_1: kuartil bawah
• Q_2: median
• Q_3: kuartil atas

Quartil

Contoh : 

9, 2, 8, 6, 5, 4, 7, 3, 1, 10

• Q_1 = x_2,75=x_2+0,75 (x_3-x_2 )=2+0,75=2,75 
• Q_2 = ? 
• Q_3 = ?

Five-Number Summary

Five-number summary: 

• Minimum 
• Q_1 
• Q_2 (m) 
• Q_3 
• Maksimum 

Graf : boxplot

Boxplot

Upper fence: 

UF = Q_3 + 1.5 * ( IQR )

Lower fence: 

LF = Q_1 - 1.5 * ( IQR )

Latihan 5

Berikut ini adalah umur dari 20 orang yang menjadi subjek sebuah penelitian medis :

• Tentukanlah five-number summary dari data tersebut
• Buatah boxplot yang sesuai
• Apakah ada outlier ?

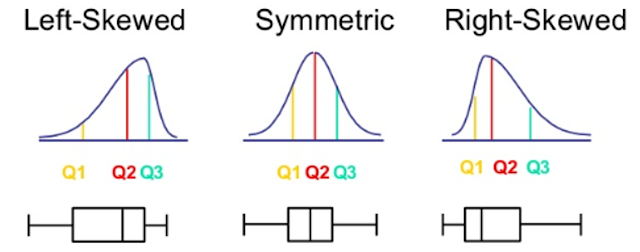
Boxplot Distribution

Distribusi yang simetri - > Boxplot simetri

Boxplot yang simetri tidak selalu berarti distribusi yang simetri

Latihan 6

Berikut ini adalah sampel dari 14 keluarga untuk mencatat berapa anak yang dimiliki oleh masing-masing keluarga:

1. Tentukanlah five-number summary dari data tersebut
2. Buatah boxplot yang sesuai. Apakah boxplot simetri ?
3. Buatlah histogram yang sesuai. Apakah histogram simetri ?

Simpangan baku ( Standard deviation )

Ukuran pusat: mean → sebaran data: simpangan baku

Simpangan baku: mengukur rata-rata jarak hasil pengukuran terhadap mean

Contoh : 

Mean = 3

Jarak masing-masing nilai terhadap mean ?

Rata-rata jaraknya ?

Standard Deviasi

Jika yang diukur adalah rata-rata jarak → ada kemungkinan simpangan 0 

Ukur kuadrat dari simpangan 

Rata-rata untuk kuadrat dari simpangan: variansi

Standard deviasi: √variansi 

Latihan 7

Berikut ini adalah data waktu yang dibutuhkan untuk cat merk “mawar” mengering ( dalam detik ) : 

Hitunglah simpangan baku dan variansi dari waktu kering cat merk “mawar” !

Empirical Rule

Empirical Rule: Untuk data berdistribusi “hampir“ normal: 

• Interval ( μ ± σ ) memuat kira-kira 68% hasil pengukuran 
• Interval ( μ ± 2σ ) memuat kira-kira 95% hasil pengukuran 
• Interval ( μ ± 3σ ) memuat kira-kira 99.7% hasil pengukuran

Umumnya: jika |z| > 2, maka x adalah outlier

Range ≈ 4s

Latihan 8

Berikut ini adalah data waktu yang dibutuhkan untuk cat merk “mawar” mengering ( dalam detik ) :

Apakah ada outlier jika menggunakan ide yang dijelaskan sebelumnya ?

Sumber

Slide Statkom : Describing Numerical Data

http://informatika.unpar.ac.id/