Matematika Dasar : Bangun Datar, Rumus Bangun Datar, Pembuktian Rumus, dan Contoh Soal
Keliling dan Luas Bangun Datar
Keliling ( perimeter )
Jumlah sisi-sisi yang membatasi sebuah bangun datar
Luas ( area )
Ukuran dua dimensi suatu bagian permukaan yang dibatasi dengan jelas
Pembuktian Rumus Persegi

Gambar di atas merupakan gambar kumpulan persegi. Untuk membuktikan rumus luas persegi maka kita bisa memperhatikan gambar persegi yang ada diatas, dimana terdapat persegi-persegi kecil di dalam sebuah persegi yang lebih besar. kita anggap persegi-persegi kecil tersebut merupakan satuan dari persegi besar.
Dengan menganggap bahwa satu persegi kecil merupakan satu satuan, maka dapat dikatakan bahwa persegi diatas memiliki luas sebanyak jumlah semua persegi kecil atau 100 satuan persegi kecil.
Untuk lebih memudahkan perhitungan maka kita dapat menghitung luas persegi dengan cara sebagai berikut
Luas Persegi = Hasil kali jumlah satuan dari kedua sisi yang saling tegak lurus
Luas Persegi = 10 x 10 = 100 satuan
Atau dapat ditulis secara umum
Luas persegi = sisi x sisi
Pembuktian Rumus Persegi Panjang
Untuk membuktikan rumus luas persegi panjang, tidak jauh beda dengan cara membuktikan rumus luas persegi. Rumus luas persegi panjang ini pada dasarnya dibangun dari rumus luas persegi. Oleh karena itu, sebelumnya saya akan memberikan sebuah postulat, yaitu :
Pernyataan Hukum Postulat
Daerah yang dilengkapi oleh persegi, dimana setiap sisinya memiliki panjang a, maka persegi ini memiliki luasan yang sama dengan a pangkat 2.
Kemudian dari Postulat di atas menghasilkan sebuah teorema untuk Luas Persegi Panjang, yaitu :
Luas suatu persegi panjang yang panjang sisinya a dan b adalah a.b
Bukti Teorema
Misal kita konstruksikan Persegi Panjang dari suatu persegi seperti pada gambar dibawah ini.

Bedasarkan dari gambar diatas dan menurut Postulat, maka :
(a + b)^2 = Luas R1 + Luas R2 + Luas R3 + Luas R4
a^2 + 2ab + b^2 = a^2 + Luas R2 + Luas R3 + b^2
karena Luas R2 = Luas R3, berakibat :
a^2 + 2ab + b^2 = a^2 + 2 Luas R2 + b^2
2a.b = 2 Luas R2
a.b = Luas R2 = Luas Persegi Panjang ( TERBUKTI )
Pembuktian Rumus Segitiga
Segitiga memiliki banyak rumus untuk mencari luasnya. Setiap rumus memiliki waktu tersendiri untuk menggunakannya, tergantung dari soal yang diberikan.
Berikut beberapa pembuktian rumus luas segitiga:
1. Pembuktian rumus L = 1/2 (alas x tinggi)
Kasus 1 Untuk Segitiga Siku-Siku

Luas Persegi Panjang = Luas R1 + Luas R2
a.b = 2 Luas R1 ( karena Luas R1 = Luas R2 )
1/2 (a.b ) = Luas R1
dengan a = alas dan b = tinggi
sehingga
L = (1/2) x alas x tinggi
Kasus 2 Untuk Segitiga Sama Kaki

Luas Persegi Panjang = Luas R1 + Luas R2 + Luas R3 + Luas R4
2.a.t = 4 Luas R2 (karena Luas R1 = Luas R2 = Luas R3 = Luas R4)
2/4 (a.t) = Luas R1 = L
1/2 (a.t) = Luas R1 = L
dengan a := alas dan t := tinggi
sehingga
L = 1/2 (alas x tinggi)
Kasus 3 Untuk Segitiga Sembarang
Luas Persegi Panjang = Luas R1 + Luas R2
Luas R1 + Luas R2 = b.t
karena Luas R1 = Luas R2, berakibat Luas R1 = 1/2(b.t)
1/2 ((a + b).t) = 1/2(b.t) + Luas
1/2(a.t) +1/2(b.t) –1/2(b.t) = Luas
1/2(a.t) = Luas
dengan a := alas dan t := tinggi
sehingga
L =1/2( alas x tinggi)
2. Pembuktian Rumus L = √(s (s-a )(s-b)(s-c))
sin2 A + cos^2 A = 1
sin2 A = 1 – cos^2 A
sin2 A = (1 + cos A) (1 – cos A )
Ingat aturan cosinus:
Ingat bahwa s = ½ (a + b + c), maka
1. (a + b + c) = 2s
2. (b + c + a) = (a + b + c) – 2a = 2s – 2a = 2 (s – a )
3. (a + b – c) = (a + b + c) – 2c = 2s – 2c = 2 (s –c )
4. (a + c – b) = (a + c + b) – 2b = 2s – 2b = 2 (s –b )
Sehingga
Ingat bahwa luas segitiga adalah
Pembuktian Rumus Jajar Genjang
Gambar di atas merupakan sebuah jajar genjang dengan alas = a dan tinggi = t
Rumus untuk mencari Luas jajar genjang = alas x tinggi = at. Untuk membuktikan rumus tersebut maka caranya adalah sebagai berikut.
Gambar di atas adalah jajar genjang yang di bagi menjadi 3 bagian dengan masing masing bagian mempunyai luas L1, L2 dan L3. Dalam hal ini kita akan mengubah bentuk diatas dengan memindahkan bagian yang mempunyai luas L3 agar sisi miring bidang L3 berimpit dengan sisi miring bidang L1. Untuk lebih jelasnya perhatikan gambar berikut.
Gambar di atas merupakan hasil perpindahan bidang L3 dan berbentuk persegi panjang. Karena rumus untuk mencari luas persegi panjang adalah L = panjang x lebar maka rumus luas persegi panjang diatas adalah L= alas x tinggi. karena persegi panjang di atas merupakan hasil perubahan bentuk jajar genjang, maka dapat disimpulkan bahwa rumus luas jajar genjang L= alas x tinggi = at.
Pembuktian Rumus Trapesium
1. Trapesium Sama Kaki
Pada trapesium yang pertama ini, terdapat sebuah persegi panjang dan diapit oleh 2 segitiga yang sama besar. berikut pembuktiannya :
LTrapesium = Luas Persegi Panjang + 2 Luas Segitiga
LTrapesium = (a x t) + (1/2 x b x t)
LTrapesium = (1/2 x 2a x t) + (1/2 x b x t) + (1/2 x b x t)
LTrapesium = 1/2 x t x (2a + b + b)
perhatikan bahwa (2a + c + c) adalah jumlah sisi yang sejajar, berakibat
LTrapesium = 1/2 x tinggi x jumlah sisi yang sejajar
2. Trapesium Sembarang
Berbeda dengan trapesium pertama, di trapesium kedua ini persegi panjang diapit oleh dua segitiga yang tidak sama besar. Berikut pembuktiannya :
LTrapesium = Luas Persegi Panjang + Luas Segitiga1 + Luas Segitiga2
LTrapesium = (a x t) + (1/2 x b x t) + (1/2 x c x t)
LTrapesium = (1/2 x 2a x t) + (1/2 x b x t) + (1/2 x c x t)
LTrapesium = 1/2 x t x (2a + b + c)
Perhatikan bahwa (2a + b + c) adalah jumlah sisi yang sejajar, berakibat
LTrapesium = 1/2 x tinggi x jumlah sisi yang sejajar
3. Trapesium Siku-Siku
LTrapesium = Luas Persegi Panjang + Luas Segitiga
LTrapesium= (a x t) + (1/2 x b x t)
LTrapesium= (1/2 x 2a x t) + (1/2 x b x t)
LTrapesium= 1/2 x t x (2a + b)
karena (2a + b) adalah jumlah sisi yang sejajar, berakibat
LTrapesium= 1/2 x tinggi x jumlah sisi yang sejajar
Jadi,
Rumus Luas Trapesium = 1/2 x tinggi x jumlah sisi yang sejajar
Pembuktian Rumus Layang-Layang
LuasLayang-Layang = Luas S1 + Luas S2 + Luas S3 + Luas S4
karena Luas S1 = Luas S2 dan Luas S3 = Luas S4 yang merupakan Luas Segitiga, maka
LuasLayang-Layang = 1/2.a.b1 + 1/2.a.b1 + 1/2.a.b2 + 1/2.a.b2
= 1/2 x (a.b1 + a.b1 + a.b2 + a.b2)
= 1/2 x (2.a.b1 + 2.a.b2)
= 1/2 x [2.a(b1 + b2)]
= 1/2 x (a + a) x (b1 + b2)
perhatikan bahwa diagonal 1 = (a + a) dan diagonal 2 := (b1 + b2)
maka Luas Layang-Layang = 1/2 x diagonal 1 x diagonal 2
Pembuktian Rumus Belah Ketupat
Luas Belah Ketupat = Luas L1 + Luas L2 + Luas L3 + Luas L4
Perhatikan Bahwa Luas L1 = Luas L2 = Luas L3 = Luas L4 merupakan Luas Segitiga, maka
Luas Belah Ketupat = 1/2.a.b + 1/2.a.b + 1/2.a.b + 1/2.a.b)
Luas Belah Ketupat = 1/2 x (a.b + a.b + a.b + a.b)
Luas Belah Ketupat = 1/2 x (4.a.b)
Luas Belah Ketupat = 1/2 x (2.a.2.b)
Luas Belah Ketupat = 1/2 x (a + a) x (b + b)
Pembuktian Rumus Lingkaran
Untuk membuktikan rumus luas lingkaran dapat digunakan banyak cara diantaranya adalah sebagai berikut:
1. Cara Euclid
Dalam membuktikan rumus lingkaran euclid membagi lingkaran menjadi beberapa bagian sama besar. Berikut merupakan contoh gambarnya,
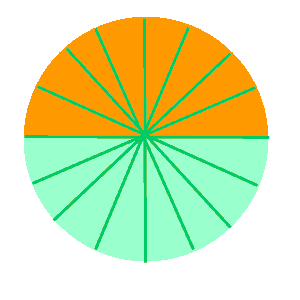
Kemudian Euclid mengaturnya menjadi bentuk jajar genjang, sebagai berikut :
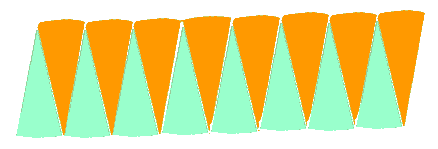
Susunan bagian lingkaran di atas menyerupai bentuk jajar genjang, dimana untuk panjang jajar genjang adalah setengah keliling lingkaran (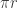 ) dan tinggi jajar genjang adalah jari-jari lingkaran (
) dan tinggi jajar genjang adalah jari-jari lingkaran ( ).
).
Karena luas jajar genjang = Luas lingkaran
Luas lingkaran = alas x tinggi
Luas lingkaran = 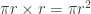
2. Dengan Integral
Perlu diketahui bahwa persamaan umum lingkaran adalah :
dengan mengambil bagian positif / atas sumbu x, maka
Latihan 1
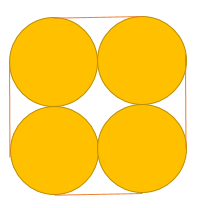
Sebuah taman berbentuk empat lingkaran identik yang memiliki jari-jari 7m dan dikelilingi oleh kawat seperti pada gambar berikut. Bagian berwarna kuning akan ditanami bunga matahari dan bagian berwarna putih akan ditanami bunga lili.
- Berapakah panjang kawat yang dibutuhkan untuk mengelilingi seluruh taman?
- Berapakah luas taman bunga matahari?
- Berapakah luas taman bunga lili?
Rumus dan Pembuktian Luas Segi-n Beraturan
 |
| Gedung Pentagon di Amerika Serikat |
Bagaimana rumus luas segi n beraturan? Bagaimana mencari rumus luas segi n beraturan? Atau bagaimana bukti umum dari rumus luas segi n beraturan. Sedikit akan bahas mengenai segi n beraturan, entah itu segitiga, segiempat, segi lima, segi enam, segi tujuh, segi delapan, dan lainnya.
Untuk mencari luas suatu bangun datar (poligon), yang kita lakukan biasanya adalah mencari luas segitiga-segitiga kecil yang menyusun poligon tersebut. Tentunya kita tahu bagaimana rumus suatu segitiga. Banyak sekali rumus-rumus untuk mencari luas segitiga.
Semua inti dari rumusnya adalah
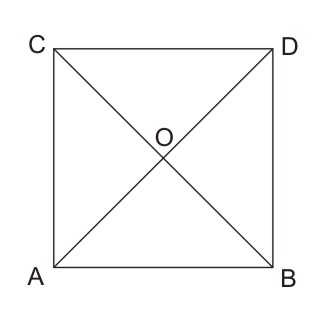
Bagaimana caranya untuk mencari luas bangun datar tersebut?
Bentuk bangun datar tersebut adalah bentuk persegi. Yang panjang setiap sisinya adalah sama. Perhatikan persegi tersebut. Kita bisa memandangnya sebagai 4 buah segitiga. Yaitu segitiga ABO, segitiga BOD, segitiga DOC dan segitiga COA.. Bentuk persegi tersebut adalah segi empat yang beraturan. Mempunyai panjang DO, CO, AO, BO sama.
Lalu bagaimana mencari luasnya dengan mencari luas segitiga yang membentuknya?
Luas masing-masing segitiga tersebut adalah sama. Karena bangun datar ini adalah segiempat beraturan (persegi). Luas AOB sama dengan
Sehingga luas segi empat beraturan adalah
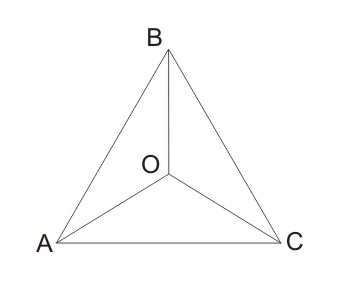
Bagaimana untuk segitiga beraturan ?
Sama halnya dengan segiempat beraturan. Untuk mencari luas segitiga beraturan juga bias didapatkan dari mencari luas segitiga yang membentuknya. Luas AOB sama dengan
Sehingga luas segi tiga beraturan adalah
Perhatikan lagi untuk luas segiempat beraturan.
Bentuk tersebut juga bias dituliskan
Karena
Dari konsep tersebut, kita bisa menentukan rumus untuk segi lima beraturan, segi enam beraturan, segi tujuh beraturan, segi delapan beraturan, dan luas segi n beraturan. Yaitu sebagai berikut.
Itu adalah rumus untuk segi-n beraturan. Jadi, untuk segitiga, ganti n dengan 3. Untuk segi empat, ganti n dengan empat. Untuk segilima, ganti n dengan 5, untuk segi enam, ganti n dengan 6, dan seterusnya. Ingat! ini hanya berlaku untuk segi n yang beraturan. Artinya, setiap sisinya mempunyai panjang yang sama. r di sini adalah jarak pusat segi n dengan titik pada perpotongan sisi-sisinya.
Latihan 2
- Luas suatu persegi 36 cm2. Panjang diagonal tersebut adalah ….
- Keliling persegi sama dengan keliling persegipanjang, panjang sisi persegi 12 cm dan lebar persegipanjang 6 cm, maka panjang persegipanjang tersebut adalah ….
- Suatu persegi ABCD diketahui kelilingnya 64 cm. Luasnya adalah ….
- Keliling trapesium samakaki adalah 50 cm. Panjang sisi-sisi yang sejajar 9 cm dan 21 cm. Luas trapesium adalah ….
- Belahketupat PQRS dengan panjang diagonal 8 cm dan 6 cm. Keliling belahketupat tersebut adalah ….
- Belahketupat ABCD mempunyai keliling 100 cm dan panjang salah satu diagonalnya 40 cm. Luas belahketupat tersebut adalah ….
- Luas segitiga samakaki dengan alas 10 cm dan keliling 36 cm adalah ….
- Suatu belahketupat luasnya 96 cm2. Panjang salah satu diagonalnya 16 cm. Keliling belahketupat tersebut adalah ….
- Keliling suatu belahketupat 52 cm, panjang salah satu diagonalnya 24 cm. Maka luas belahketupat tersebut adalah ….
- Hitunglah luas suatu bangunan X dengan bentuk segi-7 beraturan yang panjang sisinya 72 meter !






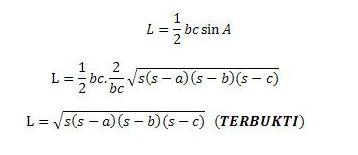







itu dari semester 1 ?
BalasHapusMantap
BalasHapusThanks gan infonya visit back. zonanesia
BalasHapuslagu edm terbaik
template blogger gratis keren
Posting Komentar